Urban Traffic Modeling and Control
Robust modeling and control of urban traffic network
The growth of the motorization rate together with the external consequences generates real challenges for the traffic planners and traffic engineers. For example, today’s demand is not satisfied by a traffic-responsive traffic light depending on detector measurements. To assure the sustainable mobility as well a suitable life quality in cities a complex strategy and a network-wide traffic control are needed. The intelligent and adaptive road traffic control realizes a classical control loop practically: measurement, estimation, control, reaction (Fig. 1).
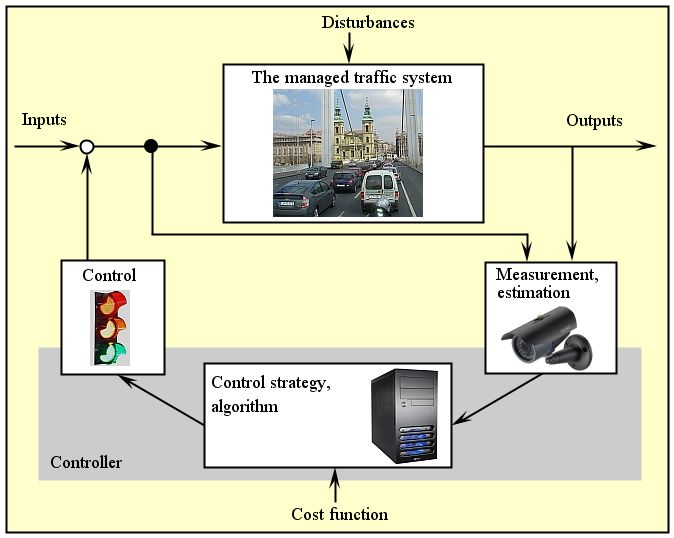
Figure 1: Control loop in the road traffic management
If the states of the traffic network are known model-based control can be designed. Naturally, several - already existing and functioning - methods are available in this field, which aim to increase the capacity and improve other traffic parameters. One of the first approaches using modern control theory for network-wide traffic control was published by Diakaki et al. (1999) by applying Linear Quadratic (LQ) optimization. As a further development several papers introduced the application of Model Predictive Control (MPC) in road traffic (Tettamanti et al., 2008, Aboudolas et al., 2009). Moreover, decentralized realizations of MPC were also presented (de Oliveira & Camponogara, 2010, Tettamanti & Varga, 2010). These methods represent large amelioration compared to the traditional fixed-time control. However, they are not able to deal with state uncertainties (non-measurable traffic flow, e.g. parking, side street traffic) which may be present even in case of a measurement system with good quality (Fig. 2). Hence, our research aim is to find and analyze an appropriate strategy with robust properties for control of urban traffic networks (Tettamanti et al., 2014).
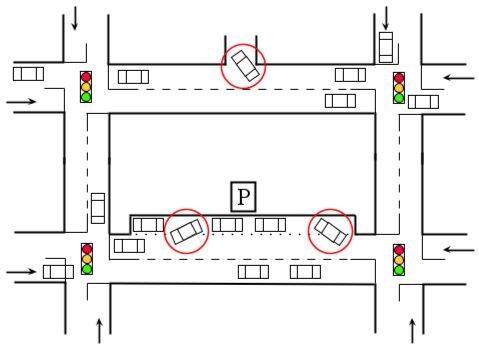
Figure 2: Typical model uncertainties in urban road traffic: side streets, parking lots
A novel approach to the control of urban traffic with uncertainty is represented by the use of robust MPC (Model Predictive Control). Practically, the method consists of a minimax optimization process in a rolling-horizon framework (Löfberg, 2003). The minimax traffic control intends to minimize the vehicle queue length while the maximal potential ambiguity is also taken into account. The rolling-horizon framework means that controller predicts the states (queue lengths) and optimal control inputs for severeal sample times. Naturally, at the end of the given sample time only the green times of the first horizon are applied. Then, the system goes on for the next step and calculates repeatedly (Fig. 3).
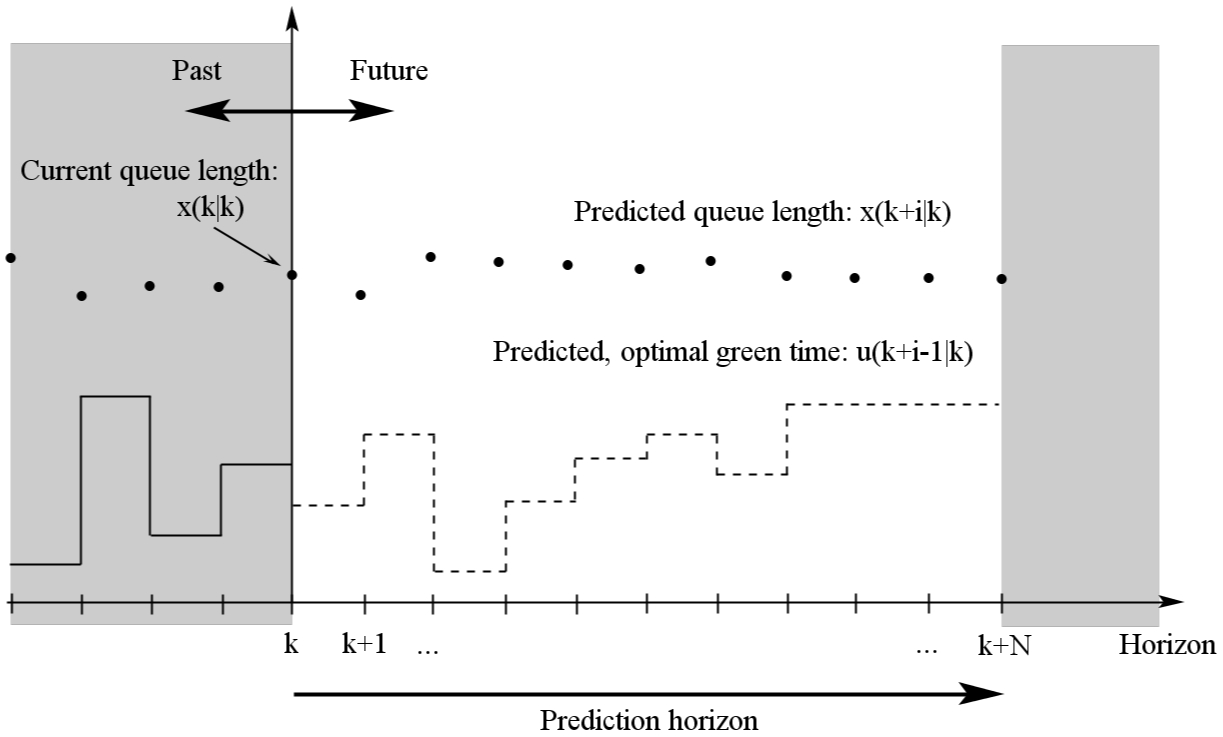
Figure 3: The predictive control scheme
The robust MPC strategy presented above was validated by real-world traffic data with VISSIM traffic simulator. A test network was created based on a part of the topology of VI. District of Budapest (Fig. 4). The control algorithm was implemented in MATLAB, which represents an SDP optimization practically. The whole simulation environment incorporates the traffic simulation, measurement, and control in a closed-loop (Tettamanti & Varga, 2012). The uncertainties were modeled as traffic flows of parking lots and side streets in the simulation. The results justify the raison d'etre of the robust strategy. An improvement of ~10-30% in traffic parameters was achieved compared to the traditional control methods. A closed-loop traffic control can be realized which is able to provide optimal signal splits in a real-time fashion even if traffic disturbances are present. Therefore, the performance of the urban traffic can be increased and congestions avoided. The theory of the method is provided in our book Forgalomirányítás (Traffic control) (Luspay et al., 2011). Further research consists of realizing the robust urban traffic control in a decentralized system.
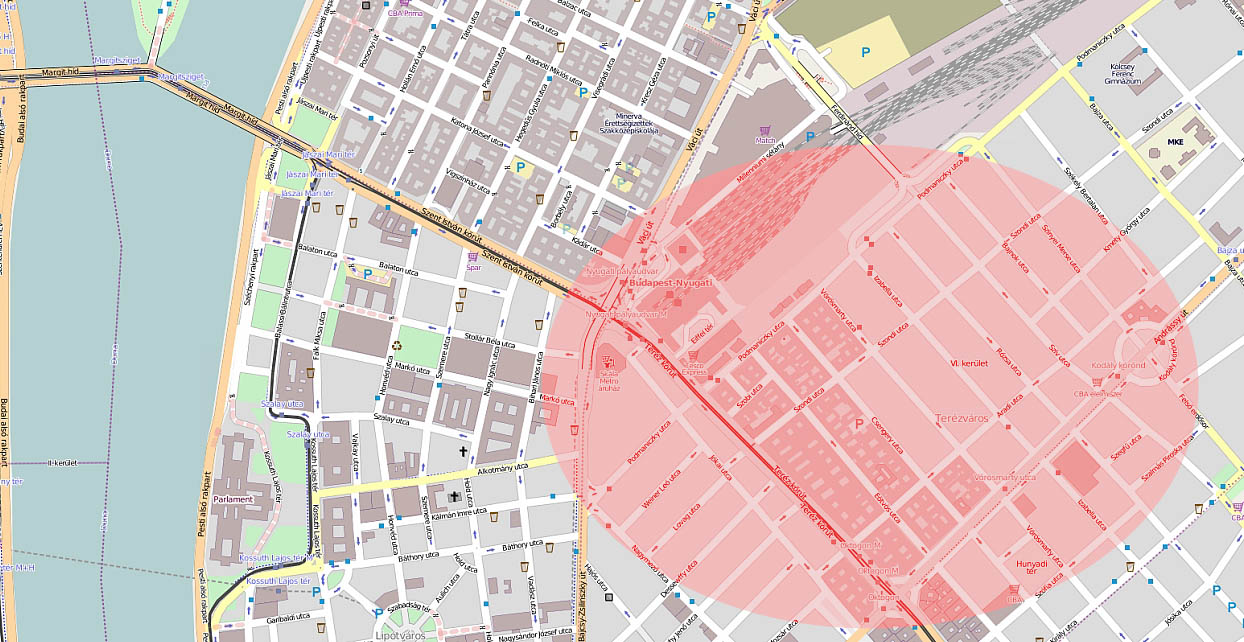
Figure 4: Test network in Budapest, District VI.
Related publications
Luspay, T., Tettamanti, T., Varga I.: Forgalomirányítás, Közúti járműforgalom modellezése és irányítása. Typotex Elektronikus Kiadó Kft. ISBN 978-963-279-665-9, 2011.
Tettamanti, T., Varga, I., Kulcsár, B., Bokor, J.: Model predictive control in urban traffic network management. In 16th Mediterranean Conference on Control and Automation, pages 1538–1543, Ajaccio, Corsica, France, 2008. CD ISBN: 978 1 4244 2505 1.
Tettamanti, T., Varga, I.: Distributed traffic control system based on model predictive control, Periodica Polytechnica ser. Civil. Eng., Budapest, Hungary, 2010, Vol. 54/1. pp. 3-9. doi: 10.3311/pp.ci.2010-1.01
Tettamanti, T., Varga, I.: Development of road traffic control by using integrated VISSIM-MATLAB simulation environment. Periodica Polytechnica ser. Civil. Eng., Budapest, Hungary, 2012, Vol. 56., in press
Tettamanti T, Luspay T, Kulcsár B, Péni T and Varga I (2014), "Robust Control for Urban Road Traffic Networks", IEEE Transactions on Intelligent Transportation Systems. Vol. 15(1), pp. 385-398.
References
Aboudolas, K., Papageorgiou, M., Kouvelas, A., Kosmatopoulos, E.: A rolling-horizon quadratic-programming approach to the signal control problem in large-scale congested urban road networks. Transportation Research Part C: Emerging Technologies, 18(5):680–694, 2010. Applications of Advanced Technologies in Transportation: Selected papers from the 10th AATT Conference.
Diakaki, C., Papageorgiou, M., Aboudolas, K.: Traffic-responsive urban network control using multivariable regulators. In International Conference on Modeling and Management in Transportation, Vol. 2, pp. 11-16, Poznan/Cracow, 1999.
Löfberg, J.: Minimax approaches to robust model predictive control. Ph.D. thesis. Linköping University, Sweden, 2003.
de Oliveira, L. B., Camponogara, E.: Multi-agent model predictive control of signaling split in urban traffic networks. Transportation Research Part C: Emerging Technologies, 18(1):120-139, 2010. Information/Communication Technologies and Travel Behaviour; Agents in Traffic and Transportation




















